[BOJ] 백준 2150번: Strongly Connected Component

https://www.acmicpc.net/problem/2150

2150번: Strongly Connected Component

 

강한 연결 요소 (SCC, Strongly Connected Component) 알고리즘은, v에서 u로가는 경로가 있을 때, 반대로 u에서 v로 갈 수 있는 경로가 존재하는 최대의 그룹 크기를 찾는 알고리즘입니다.

코사라주 알고리즘과 타잔 알고리즘으로 강한 연결 요소를 찾을 수 있는데, 본 포스팅에서는 코사라주 알고리즘에 대하여 설명합니다.

 

코사라주 알고리즘은 두번의 DFS를 수행하여 O(V+E) 복잡도로 동작합니다. ( V : 노드의 개수, E : 간선의 개수)

첫번째 DFS는 방문하지 않은 정점 v로부터 깊이 우선 탐색을 시작하여 더이상 방문할 노드가 없는 노드 u를 찾는 순간 노드에 고유한 아이디 num 값을 부여합니다.

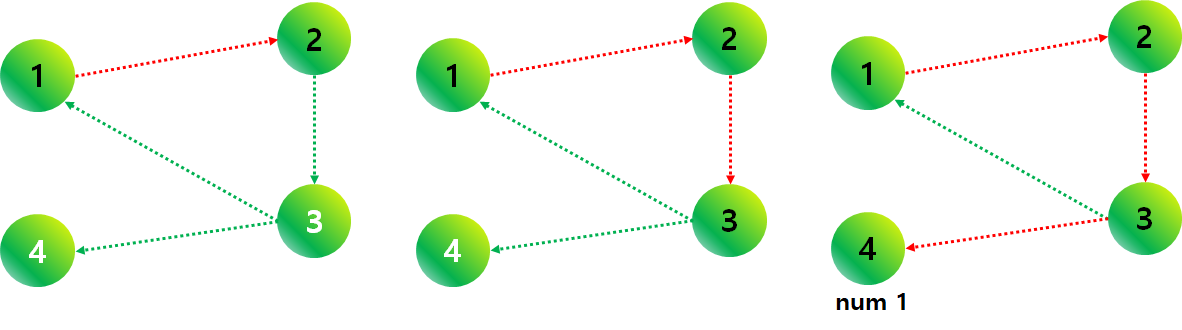
더이상 u 노드가 없다면 이전 노드로 돌아와 증가된 num 값을 부여하면서 모든 정점에 대하여 DFS를 수행합니다.

---

두번째 DFS는 간선의 역방향으로 DFS를 진행하는데,

num값이 큰 노드 v 부터 순서대로 수행하여 이전에 scc를 이루지 않은 노드 중 이미 방문된 노드 u 까지 scc가 됩니다. 아래 그림에선 1번, 2번, 3번 노드가 scc를 이루며, 남은 4번은 이전에 scc를 이룬 3번 노드로 갈 수 없기 때문에 DFS가 종료되어 혼자 scc를 이루게 되므로 총 2개의 scc가 존재하는 것을 확인할 수 있습니다..

---

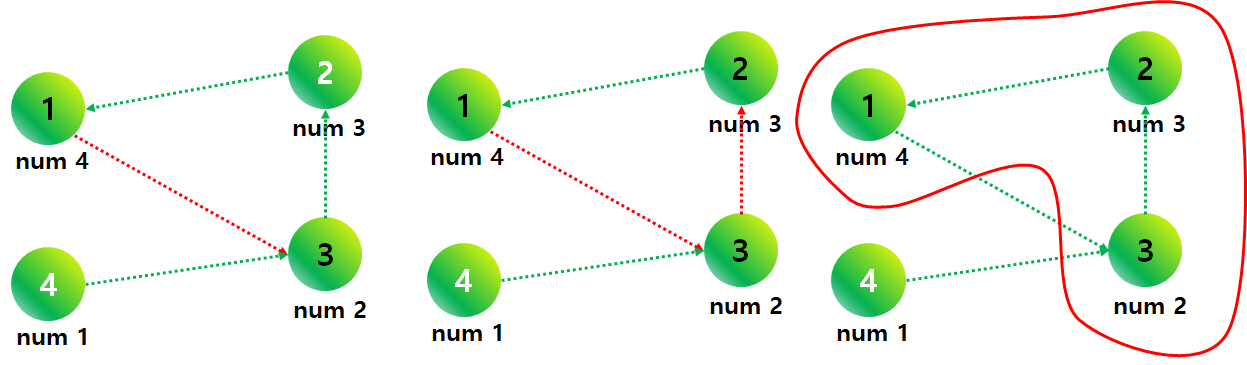
num 값의 의미를 살펴보자면... 단방향 그래프에서는 어느 지점에서 시작하든 같은 num 값을 갖습니다. num 값이 큰 순서대로 두번째 DFS를 진행하므로 (아래 그림에서 역방향으로), 위의 단순 경로에서는 3개의 scc가 존재하는 것을 볼 수 있습니다.

그러나, 아래의 그래프의 경우 두번째 DFS에서 1번 -> 3번 -> 2번을 거쳐 1번 노드 (다른 scc에 속하지 않은 이미 방문된 정점)을 만났으므로 DFS를 수행하면서 방문한 모든 노드가 하나의 scc를 구성하는 것을 볼 수 있습니다.

아래 코드는 코사라주 알고리즘에 대하여 구현한 결과이며 문제에서 오름차순으로 출력하는 조건이 있어서 유니온 파인드를 사용하여 같은 scc에 속하는 정점을 작은 노드 번호를 기준으로 묶어준뒤 출력하였습니다.

#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>

using namespace std;
typedef long long ll;

int n, m;
int visit[10001];
vector<int> v[10001];
vector<int> rv[10001];
pair<int, int> num[10001];
int p[10001];
int gnum = 1;
int gp(int x) {
	return (p[x] == x ? x : p[x] = gp(p[x]));
}
void Un(int a, int b) {
	a = gp(a);
	b = gp(b);
	if (a < b) {
		p[b] = a;
	}
	else p[a] = b;
}
void dfs(int node) {
	visit[node] = 1;
	for (auto nxt : v[node]) {
		if(!visit[nxt])
			dfs(nxt);
	}
	num[node] = {gnum, node};
	gnum += 1;
}
void dfs2(int node,int p) {
	visit[node] = p;
	for (auto nxt : rv[node]) {
		if (!visit[nxt]) {
			visit[nxt] = p;
			Un(p, nxt);
			dfs2(nxt, p);
		}
	}
}
int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		int a, b;
		cin >> a >> b;
		v[a].push_back(b);
		rv[b].push_back(a);
	}
	memset(visit, 0, sizeof(visit));
	for (int i = 1; i <= n; i++) {
		if (!visit[i]) {
			dfs(i);
		}
		p[i] = i;
	}
	sort(num, num + 1+ n);
	int ans = 0;
	memset(visit, 0, sizeof(visit));
	for (int i = n; i > 0; i--) {
		int node = num[i].second;
		if (!visit[node]) {
			ans += 1;
			dfs2(node, node);
		}
	}
	vector<int> scc[10001];
	for (int i = 1; i <= n; i++) {
		scc[gp(i)].push_back(i);
	}
	cout << ans << "\n";
	for (int i = 1; i <= n; i++) {
		if (scc[i].empty()) continue;
		for (auto nxt : scc[i]) {
			cout << nxt << " ";
		}
		cout << "-1\n";
	}
}