https://www.acmicpc.net/problem/1002
1002번: 터렛
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
www.acmicpc.net
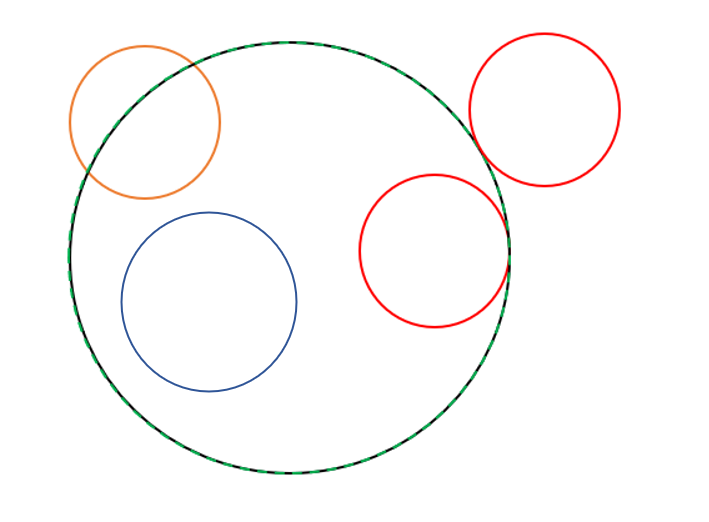
두 원의 중심과 반지름이 주어질 때, 두 원의 교점의 개수를 구하는 문제입니다.
소수점 연산의 오차를 줄이기 위하여 두 점사이 거리의 제곱을 활용합니다.
두 원의 중심 간의 거리 dist = (x1-x2)^2 + (y1-y2)^2
두 반지름의 합 sumr = (r1 + r2) * (r1 + r2)
두 원의 반지름 중 큰 것 r1, 작은것 r2 (같으면 순서 상관 없음)
1. 동심원의 경우
if (!dist) { // 동심원
cout << (r1 == r2 ? -1 : 0) << "\n";
continue;
}

2. 내접원 or 외접원
if (dist == sumr || dist == (r1-r2)*(r1-r2)) { // 외접원 or 내접원
cout << 1 << "\n";
continue;
}
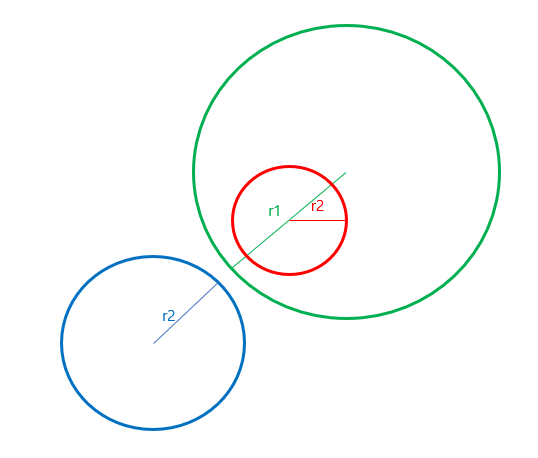
3. 만나지 않음
반지름 길이의 합보다 중점사이의 길이가 멀거나, 두 반지름의 차이보다 중점사이의 거리가 짧으면 만날수 없습니다.
if (dist > sumr || dist < (r1-r2)*(r1-r2)) {
cout << 0 << "\n";
continue;
}
4. 그 외
1~3 케이스 이외의 두 원의 관계는 무조건 두점에서 접합니다.
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int t;
cin >> t;
for (; t--;) {
ll x1, y1, r1, x2, y2, r2;
cin >> x1 >> y1 >> r1 >> x2 >> y2 >> r2;
ll dist = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
ll sumr = (r1 + r2) * (r1 + r2);
if (!dist) { // 동심원
cout << (r1 == r2 ? -1 : 0) << "\n";
continue;
}
if (dist == sumr || dist == (r1-r2)*(r1-r2)) { // 외접원 or 내접원
cout << 1 << "\n";
continue;
}
if (dist > sumr || dist < (r1-r2)*(r1-r2)) {
cout << 0 << "\n";
continue;
}
cout << 2 << "\n";
continue;
}
}반응형
'알고리즘' 카테고리의 다른 글
| [BOJ] 백준 1007번: 벡터 매칭 (0) | 2020.08.11 |
|---|---|
| [BOJ] 백준 1004번: 어린 왕자 (0) | 2020.08.11 |
| 유니온 파인드 (Union Find) 혹은 분리 집합 (Disjoint Set) (0) | 2020.08.09 |
| [BOJ] 백준 1956번: 운동 (0) | 2020.08.09 |
| [BOJ] 백준 9370번: 미확인 도착지 (0) | 2020.08.09 |



