머지 소트 트리를 이용한 백준 문제 풀이 수열과 쿼리 1 , 수열과 쿼리 3 , 트리와 색깔 , K번째 수 는 맨 아래를 참고해주세요. 코드 스포일러를 방지하기 위해 접은 글로 풀이를 남겼습니다.
알고리즘에서 c++의 algorithm 헤더에 있는 내장 sort함수는 코드의 간결성과 실수를 줄여줍니다. 그러나, 내장함수가 있다고해서 정렬 알고리즘을 구현할줄 몰라도 되는 것은 아닙니다.
아래의 버블 소트는 알고리즘 입문자들이 대부분 알고있는 정렬 알고리즘으로 O(N^2)의 비효율적인 복잡도로 작업을 수행합니다. 모든 수를 비교하면서 큰 수를 뒤로 보내는 단순한 방식으로 동작합니다.
// 버블 소트
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n; j++) {
if (arr[i] > arr[j]) {
arr[i] ^= arr[j] ^= arr[i] ^= arr[j];
// 또는 swap(arr[i],arr[j]);
}
}
}만약 다음과 같은 문제가 주어진다면 어떻게 풀 수 있을까요.
Q. a1, a2, ..., an의 배열 A가 있을때 1 <= i < j <= n 이면서 a[i] > a[j] 인 쌍의 개수를 찾아라.
이 문제는 다시 말하면 정렬을 진행하면서 앞의 원소보다 뒤의 원소가 작은 경우, 즉, swap이 일어난 횟수와 같습니다. 배열 A가 아래와 같을때를 생각해 봅시다.

1은 제일 작은 수가 맨 앞에있으므로 swap이 발생하지 않기 때문에 1을 포함한 쌍의 개수는 0입니다.
4의 경우, 2와 3 2개의 수보다 크기 때문에 swap은 2번 발생합니다. 즉 2개의 쌍에 포함됩니다.
2는 j에 대하여 쌍을 이루지 않습니다. 그러나 4와 쌍을 이루기 때문에 1개의 쌍에 포함됩니다. (중복)
5는 3보다 크기 때문에 한번의 swap이 발생합니다. 즉 1개의 쌍에 포함됩니다.
3은 마지막이므로 비교를 할 수 없습니다 ( i < j <= n)
전체 쌍의 개수는 3개입니다.
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int arr[5] = { 1,4,2,5,3 };
for (int i = 0; i < 5; i++) {
for (int j = i + 1; j < 5; j++) {
if (arr[i] > arr[j]) {
cout << "SWAP : " << arr[i] << " <> " << arr[j] << "\n";
arr[i] ^= arr[j] ^= arr[i] ^= arr[j];
// 또는 swap(arr[i],arr[j]);
}
}
}
}
근데 만약 N의 크기가 10만인 경우 O(N^2) = 10^10 = 100억이므로 너무 오래걸립니다. 그럼 좀더 빠른 정렬 알고리즘을 통해 swap 횟수를 더 빠르게 계산할 수 있다면 어떨까요.
대게 정렬 알고리즘은 O(NlgN) 복잡도를 갖습니다. 기수정렬 (Radix sort)의 경우는 O(N)의 복잡도로 수행됩니다. 그러나 자리수에 따른 변수가 (공간 복잡도 등) 있으며 음수 정렬이 어려우므로 통용되는 복잡도인 O(NlgN) 정렬을 대회에서 허용 하고있습니다.
그중 저는 병합 정렬 (머지 소트, Merge sort)에 대하여 설명하고자 합니다.
병합 정렬은 말 그대로 합치면서 정렬을 하겠다라는 뜻입니다. 그러므로 구현도 상당히 간편하고 많은 알고리즘에서도 사용될 수 있습니다. (삼성 B형의 경우 stdlib.h 헤더만 허용하여 자료구조와 정렬을 구현할 줄 알아야 합니다.)
파란색 박스는 배열을 반씩 나누는 과정이고, 초록색 박스는 나눠진 박스를 순서대로 정렬을 진행하면서 병합하는 과정입니다. 즉 반씩 나누므로 깊이는 lgN이 되고, 합치는 과정에서 N개의 수를 비교하므로 NlgN의 복잡도로 정렬이 수행됩니다.
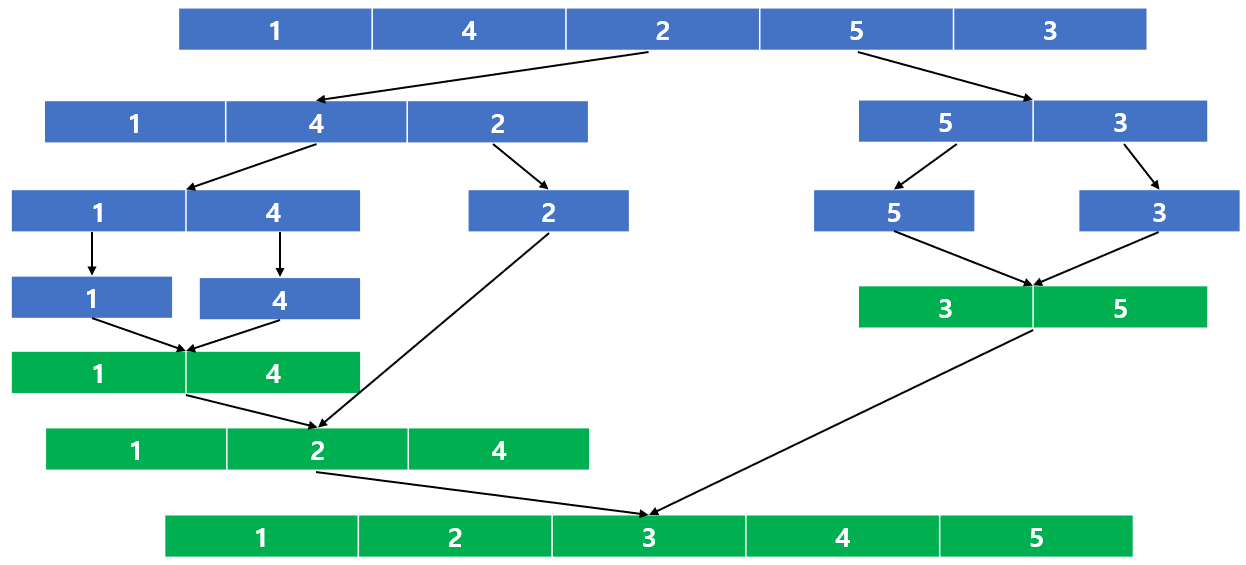
그럼 이렇게 진행되는 병합 정렬로 어떻게 a[i] > a[j]인 j의 쌍의 개수를 구할 수 있을까요.
결론부터 보자면, 처음 배열과 정렬된 배열을 서로 연결했을때 교차하는 점의 개수가 쌍의 개수랑 같습니다.
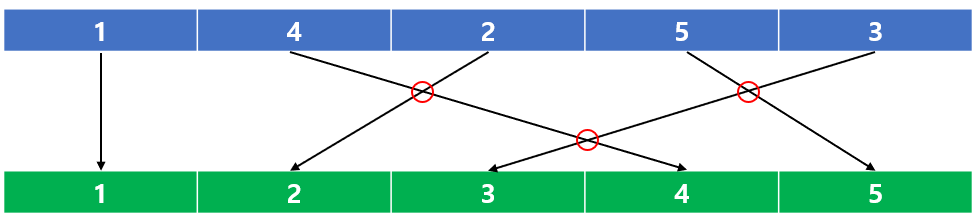
그럼 우리는 초록색 박스의 정렬과정을 수행하면서 a[i] > a[j]를 찾는 순간 교차한다고 볼 수 있습니다.
이것을 트리형태로 만들어 본다면 아래와 같습니다. 이것을 머지 소트 트리라고 합니다.

코드로는 아래와 같이 구현 할 수 있습니다. 당연히 병합 정렬 알고리즘의 복잡도와 동일한 O(NlgN)으로 교점의 개수를 구할 수 있습니다.
#include <iostream>
#include <algorithm>
#include <vector>
#include <memory.h>
using namespace std;
int mst[20][100001];
int arr[5] = { 1,4,2,5,3 };
int brr[5] = { 1,4,2,5,3 };
int number_of_cross = 0;
void mergesort(int s, int e,int d) { // 시작, 끝, 깊이
if (s == e) {
mst[d][s] = brr[s];
return;
}
int mid = (s + e) / 2;
mergesort(s, mid, d + 1);
mergesort(mid + 1, e, d + 1); // 절반씩 나눔
int left = s;
int right = mid + 1;
int idx = s;
while (left < mid + 1 && right < e + 1) { // 병합
if (mst[d + 1][left] <= mst[d + 1][right]) {
mst[d][idx] = mst[d + 1][left];
left += 1;
idx += 1;
}
else {
number_of_cross += (mid - left + 1);
mst[d][idx] = mst[d + 1][right];
right += 1;
idx += 1;
}
}
while (left < mid + 1) { // 남는것 채워줌
mst[d][idx] = mst[d + 1][left];
left += 1;
idx += 1;
}
while (right < e + 1) { // 남는것 채워줌
mst[d][idx] = mst[d + 1][right];
right += 1;
idx += 1;
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
//int arr[5] = { 1,4,2,5,3 };
//for (int i = 0; i < 5; i++) {
// for (int j = i + 1; j < 5; j++) {
// if (arr[i] > arr[j]) {
// cout << "SWAP : " << arr[i] << " <> " << arr[j] << "\n";
// arr[i] ^= arr[j] ^= arr[i] ^= arr[j];
// // 또는 swap(arr[i],arr[j]);
// }
// }
//}
int brr[5] = { 1,4,2,5,3 };
mergesort(0, 4, 0);
cout << number_of_cross << "개의 교점이 생김\n";
cout << "정렬 결과 : \n";
for (int i = 0; i < 5; i++) {
cout << mst[0][i] << " ";
}
}
만약 병합을 하는 과정에서 right가 left보다 작은 경우에 아직 정렬이 안된 left ~ mid는 현재 right보다 더 크므로 교차점을 만듭니다. 이것을 모두 더해주면서 병합 정렬을 진행하면 모든 교차점의 개수를 구할 수 있습니다.
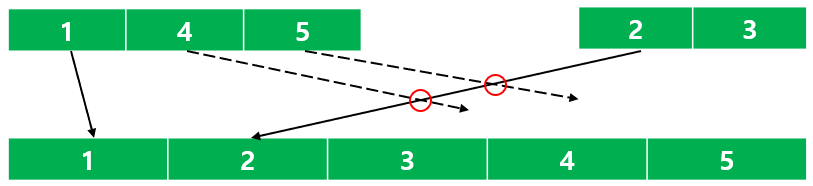
머지 소트 트리를 사용하여 풀 수 있는 문제들입니다.
13537번: 수열과 쿼리 1
길이가 N인 수열 A1, A2, ..., AN이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오. i j k: Ai, Ai+1, ..., Aj로 이루어진 부분 수열 중에서 k보다 큰 원소의 개수를 출력한다.
www.acmicpc.net
13537번: 수열과 쿼리 1은 배열의 특정 구간에서 K보다 큰 수의 개수를 찾는 문제입니다. 머지소트 트리는 구간에 대하여 정렬이 되어있기 때문에 구간에서 k보다 큰 원소를 이분탐색으로 찾을 수 있습니다.
정답코드
#include <iostream>
#include <algorithm>
#include <memory.h>
#include <vector>
#include <queue>
#include <stack>
using namespace std;
typedef long long ll;
int n, m, k;
int arr[100001];
int mst[17][100002] = { 0, };
void make_tree(int s, int e,int depth) {
if (s == e) {
mst[depth][s] = arr[s];
}
else {
int mid = (s + e) / 2;
make_tree(s, mid, depth + 1);
make_tree(mid + 1, e, depth + 1);
int i = s, j = mid + 1;
int idx = s;
while (i <= mid && j <= e) {
if (mst[depth+1][i] < mst[depth+1][j]) {
mst[depth][idx] = mst[depth + 1][i];
i += 1;
}
else {
mst[depth][idx] = mst[depth + 1][j];
j += 1;
}
idx += 1;
}
while (i <= mid) {
mst[depth][idx] = mst[depth + 1][i];
i += 1;
idx += 1;
}
while (j <= e) {
mst[depth][idx] = mst[depth + 1][j];
j += 1;
idx += 1;
}
}
}
int query(int s, int e,int depth, int num,int ds,int de) {
if (s == ds && e == de) { // 겹침
// 이분탐색 upper_bound
int _s = s, _e = e;
int mid;
while (_s <= _e) {
mid = (_s + _e) / 2;
if (mst[depth][mid] > num) {
_e = mid - 1;
}
else {
_s = mid + 1;
}
}
return e- _e;
}
int mid = (s + e) / 2;
if (mid < ds) {
return query(mid + 1, e, depth + 1, num, ds, de);
}
else if (mid >= de) {
return query(s, mid, depth + 1, num, ds, de);
}
else {
return query(s, mid, depth + 1, num, ds, mid) + query(mid + 1, e, depth + 1, num, mid + 1, de);
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
m += k;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
make_tree(1, n,0);
cin >> m;
for (; m--;) {
int s, e, c;
cin >> s >> e >> c;
cout << query(1, n, 0, c, s, e) <<"\n";
}
}13544번: 수열과 쿼리 3
길이가 N인 수열 A1, A2, ..., AN이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오. i j k: Ai, Ai+1, ..., Aj로 이루어진 부분 수열 중에서 k보다 큰 원소의 개수를 출력한다.
www.acmicpc.net
13544번: 수열과 쿼리 3은 수열과 쿼리1과 유사하지만 마지막 쿼리의 정답을 사용하여 새 쿼리를 만들어 답을 출력하는 문제입니다.
정답코드
#include <iostream>
#include <vector>
#include <algorithm>
#include <memory.h>
#include <stack>
using namespace std;
typedef long long ll;
int mst[20][100001];
int n, q;
int arr[100001];
void make_tree(int depth, int s, int e) {
if (s == e) {
mst[depth][s] = arr[s];
}
else {
int mid = (s + e) / 2;
make_tree(depth + 1, s, mid);
make_tree(depth + 1, mid + 1, e);
int l = s;
int r = mid + 1;
int idx = s;
for (; l < mid + 1 && r <= e;) {
if (mst[depth + 1][l] < mst[depth + 1][r]) {
mst[depth][idx] = mst[depth + 1][l];
l += 1;
}
else {
mst[depth][idx] = mst[depth + 1][r];
r += 1;
}
idx += 1;
}
while (l < mid + 1) {
mst[depth][idx] = mst[depth + 1][l];
l += 1;
idx += 1;
}
while (r < e + 1) {
mst[depth][idx] = mst[depth + 1][r];
r += 1;
idx += 1;
}
}
}
int query(int depth,int l,int r, int s,int e,int v){
if (l == s && r == e) {
int _s = s;
int _e = e;
int mid;
int idx = e + 1;
while (_s <= _e) {
mid = (_s + _e) / 2;
if (mst[depth][mid] > v) {
idx = mid;
_e = mid - 1;
}
else {
_s = mid + 1;
}
}
return e - idx + 1;
}
int mid = (l + r) / 2;
if (mid < s) {
return query(depth + 1, mid + 1, r, s, e, v);
}
else if (mid >= e) {
return query(depth + 1, l, mid, s, e, v );
}
else {
return query(depth + 1, l, mid, s, mid, v) + query(depth + 1, mid + 1, r, mid + 1, e, v);
}
}
int main() {
ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);
memset(mst, -1, sizeof(mst));
cin >> n;
for (int i =0 ; i < n; i++) {
cin >> arr[i];
}
make_tree(0, 0, n - 1);
cin >> q;
int last_ans = 0;
for (; q--;) {
int a, b, c;
cin >> a >> b >> c;
int i = a ^ last_ans;
int j = b ^ last_ans;
int k = c ^ last_ans;
last_ans = query(0, 0, n - 1, i-1,j-1,k);
cout << last_ans <<"\n";
}
}15899번: 트리와 색깔
M개의 질의에 대한 정답을 모두 더한 뒤, 1,000,000,007로 나눈 나머지를 출력한다.
www.acmicpc.net
15899번: 트리와 색깔은 마찬가지로 서브 루트를 머지소트 트리로 구성하여 이분탐색으로 빠르게 쿼리에 대한 답을 찾을 수 있는 문제입니다.
정답코드
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
#include <stack>
#define MOD (1000000007LL)
using namespace std;
typedef long long ll;
int n, m, c;
int color[200001];
int arr[200001];
int turn[200001][2];
vector<int> v[200001];
int idx=0;
int mst[20][200001];
void dfs(int node, int p) {
turn[node][0] = ++idx;
arr[idx] = color[node];
for (auto child : v[node]) {
if (child != p) {
dfs(child, node);
}
}
turn[node][1] = idx;
return;
}
void make_tree(int s, int e, int d) {
if (s == e) {
mst[d][s] = arr[s];
return;
}
int mid = (s + e) / 2;
make_tree(s, mid, d + 1);
make_tree(mid + 1, e, d + 1);
int ls = s;
int rs = mid + 1;
int i = s;
for (;ls < mid+1 && rs < e + 1 && i < e+ 1 ; ) {
if (mst[d + 1][ls] < mst[d + 1][rs]) {
mst[d][i] = mst[d + 1][ls];
ls += 1;
i += 1;
}
else {
mst[d][i] = mst[d + 1][rs];
rs += 1;
i += 1;
}
}
for (; ls < mid + 1;) {
mst[d][i] = mst[d + 1][ls];
ls += 1;
i += 1;
}
for (; rs < e + 1; ) {
mst[d][i] = mst[d + 1][rs];
rs += 1;
i += 1;
}
return;
}
int query(int start,int eend, int d,int s, int e, int k) {
if (start == s && eend == e) {
int _s = s, _e = e;
int mid;
int cnt = -1;
while (_s <= _e) {
mid = (_s + _e) / 2;
if (mst[d][mid] <= k) {
cnt = mid;
_s = mid + 1;
}
else {
_e = mid - 1;
}
}
if (~cnt) {
return cnt - s + 1;
}
else {
return 0;
}
}
int mid = (start + eend) / 2;
if (mid < s) {
return query(mid+1, eend, d + 1, s, e, k);
}
else if (mid >= e) {
return query(start, mid, d + 1, s, e, k);
}
else {
return query(start, mid, d + 1, s, mid, k) + query(mid+1,eend,d+1,mid+1,e,k);
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> n >> m >> c;
for (int i = 1; i <= n; i++) {
cin >> color[i];
}
for (int i = 1; i < n; i++) {
int a, b;
cin >> a >> b;
v[a].push_back(b);
v[b].push_back(a);
}
dfs(1, -1);
make_tree(1, n, 0);
ll ans = 0;
for (int i = 0; i < m; i++) {
int root, k;
cin >> root >> k;
//cout << turn[root][0] << "~" << turn[root][1] << "\n";
ans += (ll)query(1,n,0, turn[root][0], turn[root][1], k);
ans %= MOD;
}
cout << ans;
}7469번: K번째 수
문제 현정이는 자료 구조 프로젝트를 하고 있다. 다른 학생들은 프로젝트 주제로 스택, 큐와 같은 기본 자료 구조를 구현하는 주제를 선택했다. 하지만, 현정이는 새로운 자료 구조를 만들었다.
www.acmicpc.net
7469번: K번째 수역시 머지 소트 트리를 사용하는 문제입니다. 특정 수 x에 대하여 x가 i~j 구간에서 몇번째 수 일지 구해가면서 만약 x 이하의 수가 k개인 경우 그 x가 답이됩니다. x를 찾는 과정은 이분탐색으로 진행하면 됩니다.
예를 들어 2 3 5 6 의 수가 있을 떄 4번째 수를 구한다하면
s = -10, e = 10을 기준으로 이분탐색을 진행하면
mid = 0 -> query(0) = 0 < 4 이므로, s = mid +1로 갱신
s = 1 , e = 10
mid = 5 -> query(5) = 3 <4 이므로, s = mid+1로 갱신
s = 6, e = 10
mid = 8 ->query(8) = 4 =4이므로, e = mid-1로 갱신
s = 6, e = 7
mid = 6 -> query(6) = 4 =4 이므로, e = mid-1로 갱신
s= 6, e =6 으로 break;
우리가 원하는 답 6을 얻을 수 있습니다,
정답코드
#include <iostream>
#include <algorithm>
#include <vector>
#include <memory.h>
using namespace std;
int mst[20][100001];
int arr[100001];
int n, m;
int number_of_cross = 0;
void mergesort(int s, int e,int d) {
if (s == e) {
mst[d][s] = arr[s];
return;
}
int mid = (s + e) / 2;
mergesort(s, mid, d + 1);
mergesort(mid + 1, e, d + 1);
int left = s;
int right = mid + 1;
int idx = s;
while (left < mid + 1 && right < e + 1) {
if (mst[d + 1][left] <= mst[d + 1][right]) {
mst[d][idx] = mst[d + 1][left];
left += 1;
idx += 1;
}
else {
number_of_cross += (mid - left + 1);
mst[d][idx] = mst[d + 1][right];
right += 1;
idx += 1;
}
}
while (left < mid + 1) {
mst[d][idx] = mst[d + 1][left];
left += 1;
idx += 1;
}
while (right < e + 1) {
mst[d][idx] = mst[d + 1][right];
right += 1;
idx += 1;
}
}
int query(int s, int e, int d, int i, int j, int x) {
if (s == i && e == j) {
int _s = s, _e = e;
int _mid;
int cnt = s-1;
// s~e 구간에서 x 이하인 수의 개수를 리턴
while (_s <= _e) {
_mid = (_s + _e) / 2;
if (mst[d][_mid] <= x) {
_s = _mid + 1;
cnt = _mid;
}
else {
_e = _mid - 1;
}
}
return cnt-s+1;
}
int mid = (s + e) / 2;
if (mid < i) {
return query(mid + 1, e, d + 1, i, j, x);
}
else if (mid >= j) {
return query(s, mid, d + 1, i, j, x);
}
else {
return query(s, mid, d + 1, i, mid, x) + query(mid + 1, e, d + 1, mid + 1, j, x);
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
mergesort(1, n, 0);
for (; m--;) {
int i, j, k;
cin >> i >> j >> k; // i~j 를 정렬했을때 k번째
// k번째 수가 먼지 모르니까 일단 x라고 해보자
int s = -1e9, e = 1e9;
int x;
int ans = 0;
while (s <= e) {
x = (s + e) / 2;
// 그럼 i~j 구간에서 x이하인 수의 개수를 구해보자
int small = query(1, n, 0, i, j, x);
if (small < k) { // x 이하인 수가 k보다 작으면
s = x + 1; // 수를 좀더 키워보자
}
else e = x - 1;
}
cout << s <<"\n";
}
}
병합 정렬은 구현도 쉽고 다양한 문제에 적용될 수 있는 정렬 알고리즘으로 꼭 다시 공부하시는것을 추천 드립니다.
'알고리즘' 카테고리의 다른 글
| 삼성 SW 기출 문제 풀이 모음 (0) | 2020.10.18 |
|---|---|
| [UCPC] B번 던전 지도, 백준 19543 (0) | 2020.08.18 |
| [BOJ] 백준 10830번: 행렬 제곱 (빠른 거듭 제곱) (0) | 2020.08.17 |
| 오일러 𝜑(피 또는 파이) 함수, 서로소 개수 구하기 (1) | 2020.08.13 |
| [BOJ] 백준 1028번: 다이아몬드 광산 (0) | 2020.08.12 |


